【演算】斐波那契數列 - Fibonacci Sequence

　　斐波那契數列(Fibonacci Sequence)得名於暱稱為 Fibonacci 的義大利數學家 Leonardo of Pisa。斐波那契數列由 0 和 1 開始，第 3 項之後的值則為前兩項之和。數學上的定義如下：

* F₀ = 0
* F₁ = 1
* F_n = F_{n - 1} + F_{n - 2} (n > 1)

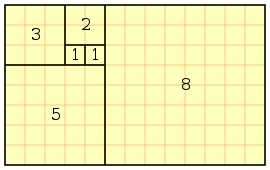
　　對電算概論而言，斐波那契數列則時常用來解釋遞迴(recursion)的概念。舉例來說，以下是以遞迴實現斐波那契數列的虛擬碼：

int Fibonacci(Index n)
{
    if      (n = 0) { return 0; }
    else if (n = 1) { return 1; }
    else
    {
        return Fibonacci(Index - 1) + Fibonacci(Index - 2);
    }
}

　　不過，這種方式雖然直覺而且簡單，但是其執行效率卻相當差。因為在需要求出 F_n (n > 1) 值的同時，我們也必須得到 F_{n - 1} 與 F_{n - 2} 的值。而為了得出 F_{n - 1} 的值，又必須再重複求出 F_{n - 2} 的值。

　　不斷重複求出同樣的值的結果，就是浪費太多的程式時間。因此只要 n 大到一個程度，程式就幾乎無法在短時間內得出結果了。


　　那麼，還有什麼方法呢？

　　其實我們可以使用陣列搭配迴圈來做到。請看以下虛擬碼：

void Fibonacci(Index n)
{
    Index i;

    F[0] = 0;
    F[1] = 1;

    for (i = 2 to n)
    {
        F[i] = F[i - 1] + F[i - 2];
    }

    print F[n];
}

　　我們也可以只利用三個變數來達成相同功能。請看以下虛擬碼：

void Fibonacci(Index n)
{
    if      (n = 0) { return 0; }
    else if (n = 1) { return 1; }
    else
    {
        Index i;

        F[0] = 0;
        F[1] = 1;

        for (i = 2 to n)
        {
            F[2] = F[0] + F[1];

            F[0] = F[1];
            F[1] = F[2];
        }

        print F[3];
    }
}

　　至於程式語言的實作，由於之前在 96 學年度北市高中資訊競賽的會議中心 (Room)已經寫過，這裡就不重複貼出了。